1、矩阵a=[1 2 3;4 5 6;7 8 9];,分别对a进行特征值分解、奇异值分解、LU分解、QR分解及Chollesky分解。





2、将矩阵a=[4 2;7 5];b=[7 1;8 3];c=[5 9;6 2];组合成两个新矩阵,组合成一个4´3的矩阵,第一列为按列顺序排列的a矩阵元素,第二列为按列顺序排列的b矩阵元素,第三列为按列顺序排列的c矩阵元素。


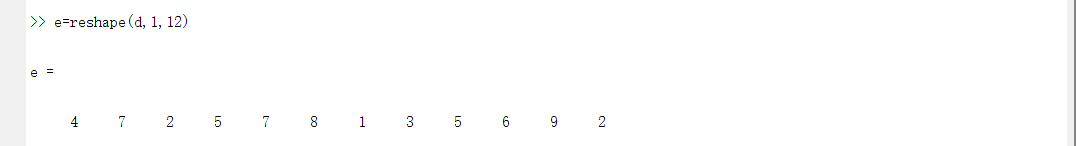
3、已知矩阵A = [3 4 -1 -9 10;6 5 0 4 -16;1 -4 7 6 -8;2 -4 5 12 -8;-3 6 -7 -1 1]。B = [1 2 6 -3 2;7 9 -5 8 -7;8 11 1 5 5;10 15 13 -1 9;2 4 -3 0 5]。b = [1 3 5 7 9]。求解矩阵方程XA=B中的解矩阵,将结果存放在变量X8中;求满足方程组AX=b’的解向量,将结果存放在变量X9中;求X8的特征值和特征向量,将特征向量组存放在变量X10中,相应的特征值记为D;



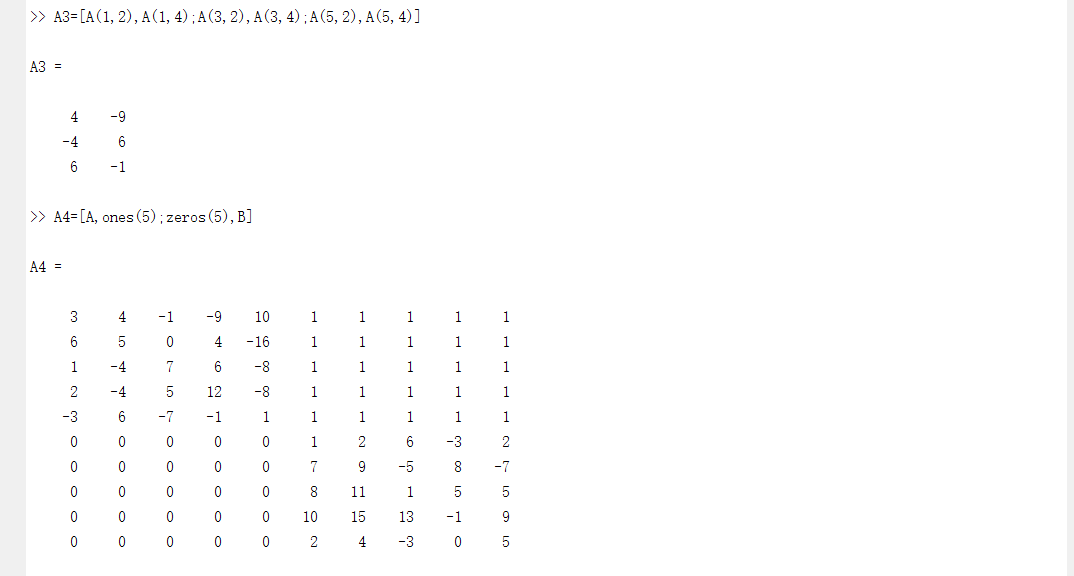
4、生成矩阵A的行向量组:a1,a2,a3,a4,a5;由A的1、3、5行,2、4列交叉点上的元素生成A的子矩阵A3;生成一个10阶矩阵A4,其左上角为A,右上角为5阶单位阵,左下角为5阶零矩阵,右下角为B;将A对应的行向量组正交规范化为正交向量组A5,并验证所得结果;完成以下初等变换:将A的第一、四行互换,再将其第三列乘以6;求B的列向量组的一个极大无关向量组A9。求矩阵A的欧几里德范数,2条件数。




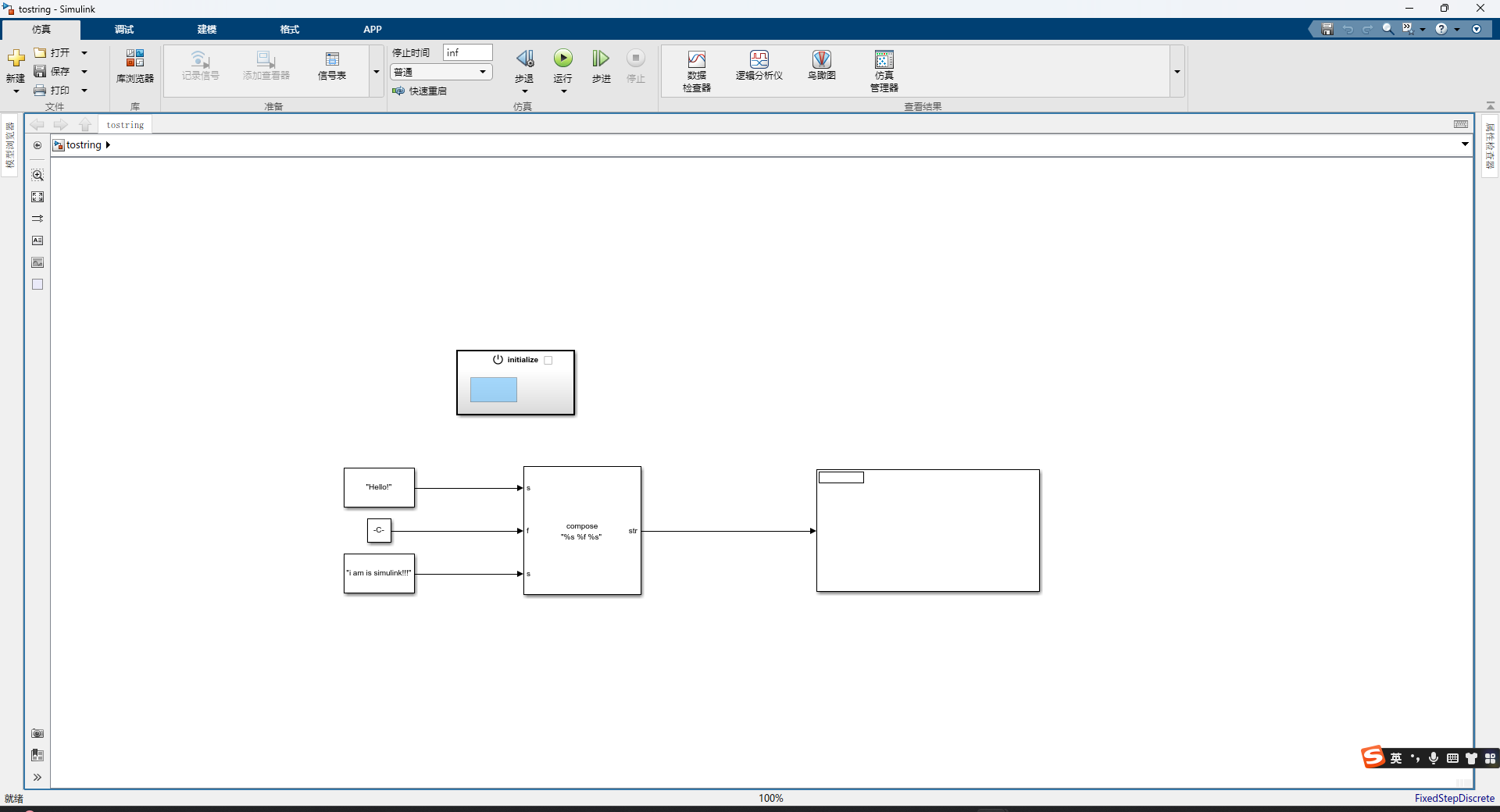
【北京德天驰鼎科技有限公司:simulink硬件解决方案+项目定制开发】